8  🍳 Simple optimal flights

8.1 Quick start

Example code to generate a fuel-optimal flight between two airports. First, we need to set up a few parameters, including origin, destination, actype, and m0 (initial mass).

The initial mass m0 can be the fraction of the maximum take-off mass (between 0 and 1), or it can be the mass in kg (for example, 65000 kg).

from openap import top

actype = "A320"
origin = "EHAM"
destination = "LGAV"

# initial mass as the faction of maximum takeoff mass
m0 = 0.85

In this simple example, we will generate a complete flight using top.CompleteFlight(). We will generate a fuel-optimal flight by setting objective to "fuel" in the trajectory generation function.

optimizer = top.CompleteFlight(actype, origin, destination, m0=m0)

flight = optimizer.trajectory(objective="fuel")
flight.head()
ts x y h latitude longitude altitude mach tas vertical_rate heading mass fuel
0 0.0 -652425.011696 840651.921623 30.480000 52.316584 4.746242 100.0 0.3000 198.38 1155.0 129.51 66300.000000 323.467557
1 240.0 -633557.291544 825095.442439 1436.228097 52.198625 5.049372 4712.0 0.5000 325.34 1655.0 137.01 65976.532443 331.368938
2 479.0 -606696.232046 796275.571353 3450.725380 51.969890 5.489660 11321.0 0.6869 436.31 2155.0 137.02 65645.163505 336.864499
3 719.0 -571079.731509 758059.040224 6073.971848 51.664098 6.066591 19928.0 0.7589 466.37 1655.0 137.02 65308.299006 310.576620
4 959.0 -532698.817232 716876.379079 8088.469130 51.331487 6.679653 26537.0 0.7970 476.69 1155.0 137.03 64997.722386 270.762600

In the previous table, we have the final fuel-optimal trajectory. Next, we can visualize the altitude, speed, and vertical rate.

import matplotlib
import matplotlib.pyplot as plt

# set up the plot styles
matplotlib.rc("font", size=11)
matplotlib.rc("font", family="Ubuntu")
matplotlib.rc("lines", linewidth=2, markersize=8)
matplotlib.rc("grid", color="darkgray", linestyle=":")


# function to make plot nicer
def format_ax(ax):
    ax.spines["right"].set_visible(False)
    ax.spines["top"].set_visible(False)
    ax.yaxis.set_label_coords(-0.1, 1.05)
    ax.yaxis.label.set_rotation(0)
    ax.yaxis.label.set_ha("left")
    ax.grid()


fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(5, 4), sharex=True)
ax1.plot(flight.ts, flight.altitude)
ax2.plot(flight.ts, flight.tas)
ax3.plot(flight.ts, flight.vertical_rate)
ax1.set_ylim(0, 40000)
ax2.set_ylim(0, 600)
ax3.set_ylim(-3000, 3000)
ax1.set_ylabel("altitude (ft)")
ax2.set_ylabel("true airspeed (kts)")
ax3.set_ylabel("vertical rate (ft/min)")
ax3.set_xlabel("time(s)")

for ax in (ax1, ax2, ax3):
    format_ax(ax)

plt.tight_layout()
plt.show()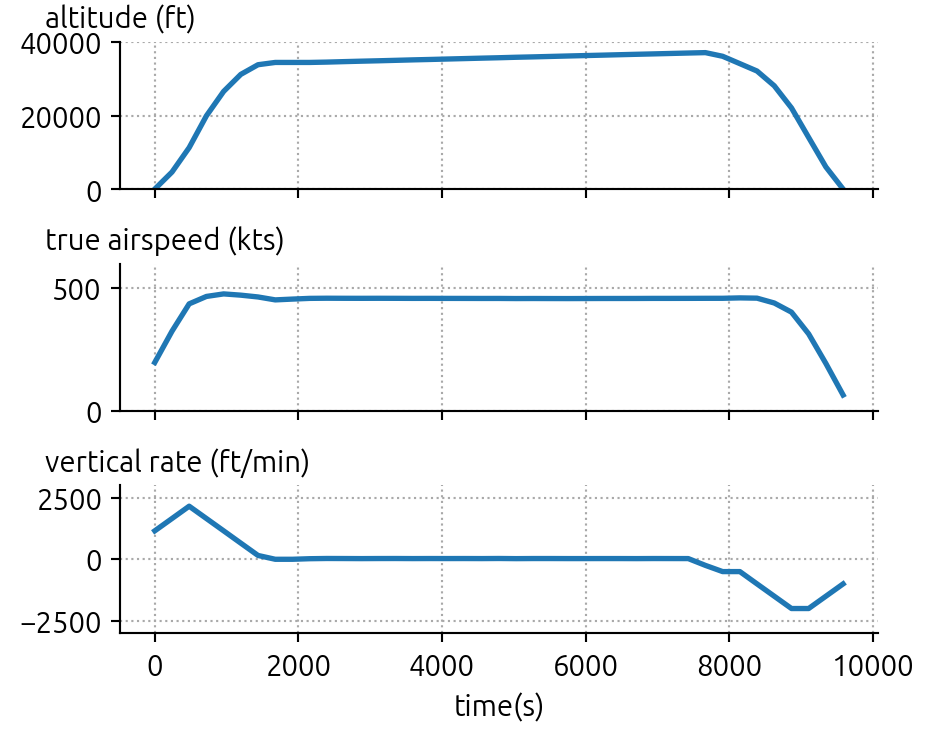

8.2 Other objective functions

Instead of the default objective functions, you can also specify different objective functions as follows:

# cost index, between 0 - 100
flight = optimizer.trajectory(objective="ci:30")

# global warming potential
flight = optimizer.trajectory(objective="gwp100")

# global temperature potential
flight = optimizer.trajectory(objective="gtp100")

The final flight object is a pandas DataFrame.

8.3 Different flight phases

Instead of generating a complete flight, we can also generate cruise, climb, and descent flights using top.Crusie, top.Climb, and top.Descent classes.

cruise_flight = top.Cruise(actype, origin, destination, m0=m0).trajectory()

climb_flight = top.Climb(actype, origin, destination, m0=m0).trajectory()

descent_flight = top.Descent(actype, origin, destination, m0=m0).trajectory()

Let’s visulize these trajectories:

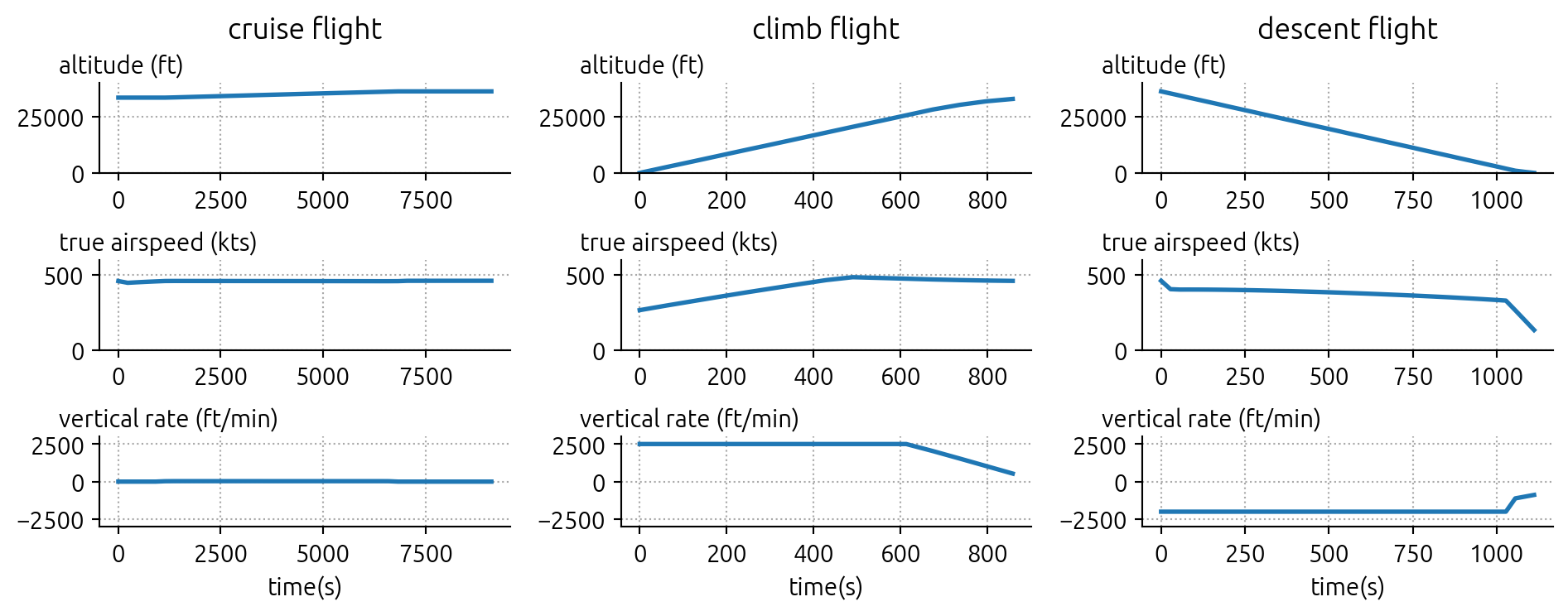
labels = ("cruise flight", "climb flight", "descent flight")

fig, axes = plt.subplots(3, 3, figsize=(10, 4))

for i, flight in enumerate([cruise_flight, climb_flight, descent_flight]):
    ax1, ax2, ax3 = axes[:, i]
    ax1.plot(flight.ts, flight.altitude)
    ax2.plot(flight.ts, flight.tas)
    ax3.plot(flight.ts, flight.vertical_rate)
    ax1.set_ylabel("altitude (ft)")
    ax2.set_ylabel("true airspeed (kts)")
    ax3.set_ylabel("vertical rate (ft/min)")
    ax1.set_ylim(0, 40000)
    ax2.set_ylim(0, 600)
    ax3.set_ylim(-3000, 3000)
    ax1.set_title(labels[i], pad=20)
    ax3.set_xlabel("time(s)")

for ax in axes.flatten():
    format_ax(ax)

plt.tight_layout()
plt.show()